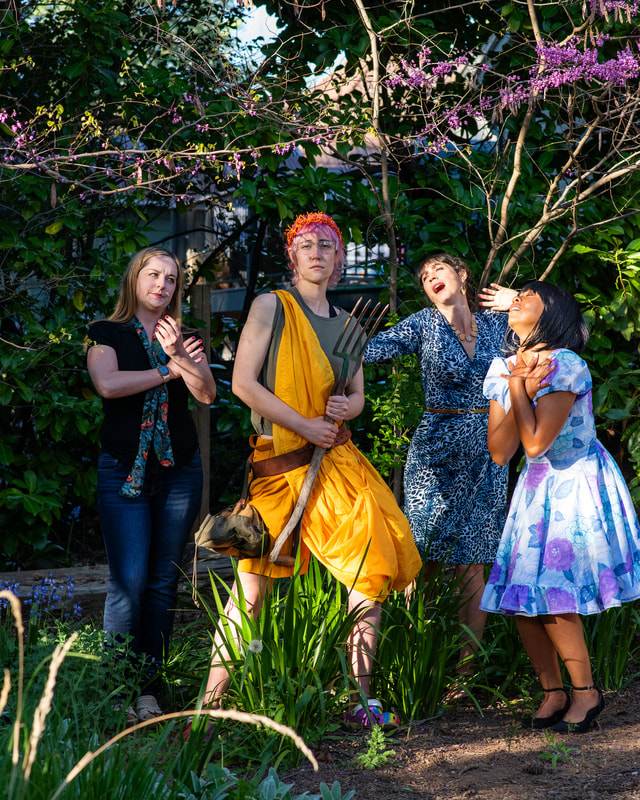THEATER BY THE BOOK is back!
HURRICANE DIANE
by Madeline George
Directed by Laura LeBleu
May 15th at the nevada theatre
Meet Diane, a permaculture gardener dripping with butch charm. She’s got supernatural abilities owing to her true identity—the Greek god Dionysus—and she's returned to the modern world to gather mortal followers and restore the Earth to its natural state. Where better to begin than with four housewives in a suburban New Jersey cul-de-sac?
Featuring - Artemis Arthur, Michaela King, Carey McRay, Jori Phillips, & Hilary Telleson
Featuring - Artemis Arthur, Michaela King, Carey McRay, Jori Phillips, & Hilary Telleson
QUACK! QUack!
Honk! is coming this summer!
July 11th - August 3rd
Honk!
music by George Stiles; book & lyrics by Anthony Drewe
Directed by Casey Burke
Honk!
music by George Stiles; book & lyrics by Anthony Drewe
Directed by Casey Burke
Opening July 2024 at The Nevada Theatre
Beauty is in the eye of the beholder in this soaring musical adaptation of Hans Christian Andersen’s The Ugly Duckling. Written by George Stiles with music and lyrics by Anthony Drewe, this heartwarming fable follows the story of Ugly, a very different kind of duckling. Ugly’s journey of self-discovery is told with love and laughter through the colorful characters he meets along the way. This family-friendly musical will bring joy to the hearts of anyone who ever felt left out or misunderstood—only to find that being different isn’t so bad after all!
Featuring: Anthony Andino, Christi Colombo, Vicki Colombo, Krissi DeKowazan, Jed Dixon, Wyndle Dixon, Heidi Grass, Mackenzie Martin, Valencia McCraner, Kenny Miele, Rorie Oas, Nori Reed, Robert Rushin and Ella Stikes
Beauty is in the eye of the beholder in this soaring musical adaptation of Hans Christian Andersen’s The Ugly Duckling. Written by George Stiles with music and lyrics by Anthony Drewe, this heartwarming fable follows the story of Ugly, a very different kind of duckling. Ugly’s journey of self-discovery is told with love and laughter through the colorful characters he meets along the way. This family-friendly musical will bring joy to the hearts of anyone who ever felt left out or misunderstood—only to find that being different isn’t so bad after all!
Featuring: Anthony Andino, Christi Colombo, Vicki Colombo, Krissi DeKowazan, Jed Dixon, Wyndle Dixon, Heidi Grass, Mackenzie Martin, Valencia McCraner, Kenny Miele, Rorie Oas, Nori Reed, Robert Rushin and Ella Stikes
October 3rd - October 19th
The Shorts
A Series of One-act Plays
The Shorts
A Series of One-act Plays
Opening September 2024 at St. Joseph’s Cultural Center
And now for something completely different! We’re gathering the best directors and actors in Nevada County for an evening of short plays that pack a punch. This collection of one acts will be fast and fun, with something for everyone!
And now for something completely different! We’re gathering the best directors and actors in Nevada County for an evening of short plays that pack a punch. This collection of one acts will be fast and fun, with something for everyone!
Sierra Stages brings home SIX Broadway World Sacramento Awards!
Congratulations to the Sierra Stages cast and collaborators who won — and thank you to everyone who voted for us!
Best Ensemble: Guys and Dolls
Best Performer in a Play: Judy Merrick, The Moors
Best Supporting Performer in a Musical: Casey Burke, Guys and Dolls
Best Supporting Performer in a Play: Chase Coney, The Moors
Best Lighting Design of a Play or Musical: Hunter Reed, The Drowning Girls
Best Sound Design of a Play or a Musical: Danny McCammon, The Drowning Girls
Best Ensemble: Guys and Dolls
Best Performer in a Play: Judy Merrick, The Moors
Best Supporting Performer in a Musical: Casey Burke, Guys and Dolls
Best Supporting Performer in a Play: Chase Coney, The Moors
Best Lighting Design of a Play or Musical: Hunter Reed, The Drowning Girls
Best Sound Design of a Play or a Musical: Danny McCammon, The Drowning Girls
Want something More?
Theatre by the Book - is an ongoing series of play readings directed by a variety of local artists. The plays are presented with a script in hand and are only performed once. Tickets are $20 and available in advance online and at the door. Play readings are on Wednesday evenings at 7 PM at the Nevada Theatre. Seating is is first-come, first-served
Out There Series - Ever wonder what’s going on out there? We do! Which is why we created our Out There series featuring new shows from beyond our borders. These daring and delightful performances deliver a dose of “wow, that was different!” to Nevada County. Their runs are short, so don’t miss out!
Have a show you'd like to share - please tell us info@sierrastages.org!
Out There Series - Ever wonder what’s going on out there? We do! Which is why we created our Out There series featuring new shows from beyond our borders. These daring and delightful performances deliver a dose of “wow, that was different!” to Nevada County. Their runs are short, so don’t miss out!
Have a show you'd like to share - please tell us info@sierrastages.org!
Thank you for supporting Sierra Stages!
IF IT WEREN’T FOR PEOPLE LIKE YOU, SIERRA STAGES WOULDN’T EXIST.
You can help us keep the spotlight on local actors & artists when you ...
Click here to join our mailing list & receive news about our productions, play readings and other local theater events!
or follow us on Facebook and Instagram for all the latest!
or follow us on Facebook and Instagram for all the latest!
Thank You 2023 Season Business Sponsors